Introducing Interactive Economics
Note to readers: I have used the LaTeX editing features of substack for the first time in the post below. If the displayed income distributions do not render correctly in your email message or browser please leave a comment to let me know and I'll avoid this in the future.
Over the past few years I have been working with a group of students at Barnard and Columbia on the development of interactive teaching resources for economics. I am thrilled to announce that Interactive Economics is now live and available for use worldwide without charge under a creative commons license.
Our first module deals with the measurement of inequality. Three other modules—on specialization and trade, technology and costs, and intertemporal choice—are in production and should be available within a month. Several other units are at various stages of completion.
No prior knowledge of economics is required to access and benefit from this material, and I have used some of it already in my introductory undergraduate course. That said, the concepts being communicated are quite technically demanding, and the interactive elements are designed to facilitate deeper understanding than is generally possible based on the conventional textbook approach.
This post describes the content and design of the first module, so that people can determine whether or not it would be useful to them.
The module on measuring inequality begins with the claim that any useful measure of inequality should allow us to compare societies with very different population sizes and levels of prosperity. It ought to help us determine whether Australia is currently more unequal than India, for example, or whether the United States is more unequal today than it was a generation ago. How might such a measure be constructed?
Consider an extremely simple example of two groups A and B with the following income distributions
Which of the two is more unequal? If we cannot come up with a logically coherent and defensible measure that allows us to answer this question, how can we expect to make convincing empirical comparisons across time and space?
There are two ways to approach the problem. One could list a set of principles (or axioms) that an inequality measure ought to satisfy and then apply these to the problem at hand. Or we could implement an existing procedure that appears intuitively to be valid, such as that proposed in the classic work of M.O. Lorenz.
It turns out that these two approaches lead to exactly the same ranking, and that is part of the point of the module.
Let’s start with the principles. Perhaps the most fundamental principle of inequality measurement is the following: if we can move from a distribution X to a distribution Y through a series of equalizing and order-preserving transfers, then Y should be judged to have less inequality than X. Such a transfer involves the movement of income from someone who has more to someone who has less, but in a manner that preserves the original ranking of people. This is known as the transfer principle, and may be illustrated with the following example
One can reach Y from X based on two equalizing and order-preserving transfers (18 from top to middle and 2 from top to bottom) so Y is less unequal than X based on the transfer principle.
But this doesn’t get us very far, because the transfer principle can only be used when the two distributions being compared have the same population size and total income.
To deal with the case of unequal aggregate income, we can use the principle of income neutrality—measured inequality remains the same if all incomes are scaled up or down by the same factor. The idea is that the measurement of inequality can be decoupled from the measurement of overall prosperity.
So, for instance, consider the distributions
Here the two distributions differ in aggregate income, but by doubling all incomes in D and then applying the transfer principle, we can see that D has a lower level of measured inequality than C.
But what if population sizes differ, as in the example with which we began? In this case one can use the principle of population neutrality, which can be explained as follows—if a set of identical component populations is pooled together to form a larger composite population, measured inequality in the composite is the same as that in each component. With this principle in hand, the problem of ranking distributions A and B can be reduced to a comparison between the following two distributions:
Here A has been “cloned” three times and B twice to get two six-person populations. The transfer principle cannot be directly applied yet because total incomes differ, but using the principle of income neutrality, we can double all incomes in the first distribution and triple all those in the second to get:
We now have two distributions with the same total income and the same population size, to which the transfer principle can be applied. Starting from the first distribution, we can transfer 3 units each from the top two individuals to the bottom two, 2 each from the top two to the fourth, and 50 from the third to the fourth. All transfers are equalizing and order-preserving, so result in a distribution with a lower level of inequality. Applying all three principles jointly, we therefore conclude that in our original example, B has less inequality than A.
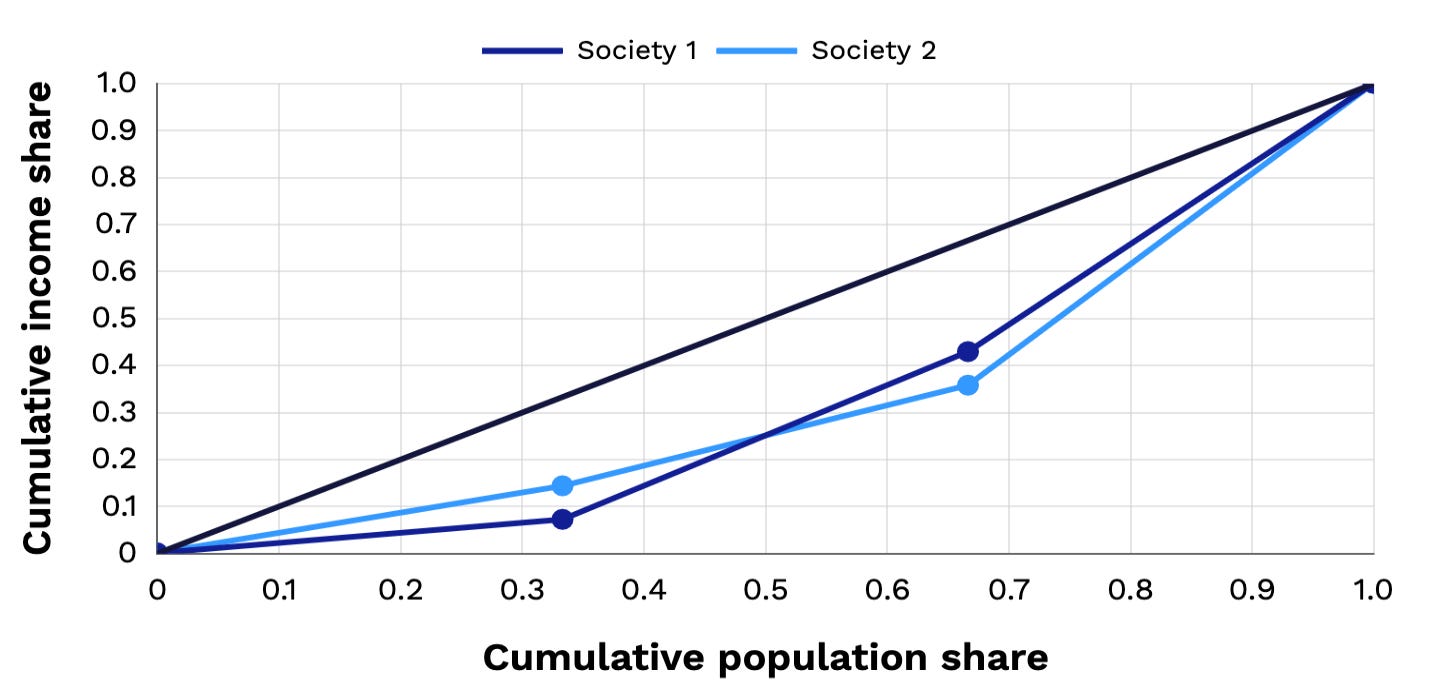
Now some might find these principles unappealing, so let’s consider an alternative approach. In an enormously influential paper published in 1905, the statistician M.O. Lorenz proposed a method of visualizing inequality that involved the following procedure. Ordering all incomes from lowest to highest, we can calculate the cumulative share of the population and the cumulative share of income held by this population as one moves up the income distribution. So in the case of the distribution A, we see that half the population has 24 percent of total income. In the case of B, the bottom one-third has 17 percent, and the bottom two-thirds collectively has 51 percent. Plotting these on the same diagram, we obtain the following Lorenz curves (this can be done using the interactive features in the module):
If all incomes were equal, the Lorenz curve would be a straight line with unit slope, as shown in the figure. We see that the Lorenz curve corresponding to distribution B lies closer to this line of perfect equality at all points than the curve corresponding to A, and based on this criterion, conclude that B has less inequality than A.
This is exactly the same answer that we obtained using the three principles, but not by coincidence! If the Lorenz criterion can rank two distributions, then so can the three principles taken together, and the rankings they produce are necessarily identical.
One can get a feel for this equivalence by seeing what happens to the curve if one scales all incomes up or down by the same factor, or clones a set of identical populations and combines them to form a composite. And one can explore the connection between the transfer principle and the Lorenz curve by examining cases where there is no way to reach one distribution from another using equalizing, order-preserving transfers. For example, plotting
yields Lorenz curves that intersect:
So these distributions cannot be ranked based on the Lorenz criterion. Nor can they be ranked based on the transfer principle—moving from F to G requires one equalizing and one dis-equalizing transfer.
There is a lot more in the module, including the introduction of the Gini coefficient, which can be used to compare distributions even when Lorenz curves cross.
In addition, users can plot curves based on actual distributions and make empirical comparisons across time and space. Here are the U.S. curves in 1980 and 2020:
And here are the curves for India and Australia in 2020:
The value of this exercise lies in exposing the deep structure that underlies such devices as the Lorenz curve, which mechanical application could not reveal. It also teaches us that our intuitions sometimes lead us astray—people who reject the principle of population neutrality may not realize, for example, that they are also rejecting the Lorenz criterion.1 And it takes students with very little prior background, who may not respond well to conventional pedagogic methods, to understand, appreciate and apply some challenging concepts in a very practical way.
I am very grateful to the Teagle Foundation, the Hewlett Foundation, and the Omidyar network for having funded this initiative, and for their early support of the closely connected CORE project. I also thank the folks at Electric Book Works who have helped us implement our vision. We hope that people will benefit from and distribute these tools, and help us to improve and expand on them over time.
A recent special issue of the Journal of Income Distribution in honor of Peter Lambert includes a debate on two versions of the Gini coefficient, only one of which is consistent with population neutrality (and hence consistent with the Lorenz criterion); for three different views on this see the contributions by me, Debraj Ray, and Sam Bowles & Wendy Carlin respectively.





Sounds interesting.