A Combinatorial Prediction Market
I'm on leave this semester, visiting Microsoft Research's recently launched New York lab. It's a lively and stimulating place and there are a number of interesting projects underway. In this post I'd like to report on one of these, a prediction market developed by a team composed of David Pennock, David Rothschild, Miroslav Dudik, Jennifer Vaughan, and Sébastien Lahaie.
This market is very different from peer-to-peer real money prediction markets such as IEM or Intrade, in that individual participants take positions not against each other but against an algorithmic market maker that adjusts prices in response to orders placed. Furthermore, a broad and complex range of events are priced, orders of arbitrary size can be met, and consistency across prices is maintained by the immediate identification and exploitation of arbitrage opportunities.
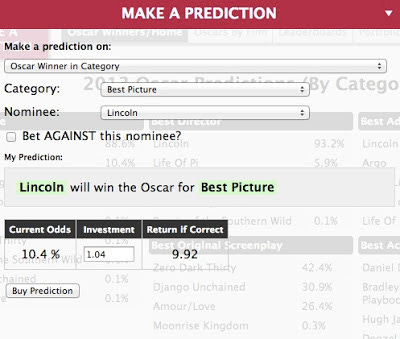
The market for Oscar predictions is now live, and it's easy to participate. You can log in with a google account (or facebook or twitter) or create a new PredictWise account. You'll be credited with 1000 points which may be used to buy a range of contracts. These include contracts on simple events, such as "Lincoln to win Best Picture." But they also include events that reference multiple categories: you can bet on the event "Argo to win Best Picture and Daniel Day-Lewis to win Best Actor in a Leading Role," or "Zero Dark Thirty to win between 3 and 5 awards" for example.
All of these contracts are priced but the price is sensitive to order size. For small orders one can buy at the currently posted odds. For instance, for "Lincoln to win Best Picture," current odds are 10.4%, so an expenditure of 0.104 units will return 1 unit if the event occurs:

But placing a larger order, say for 1.04 units, returns less than 10:
The functional relationship between the price and quantity vectors is deterministic and satisfies three conditions: (i) the purchase of a contract (or portfolio) raises its price smoothly, (ii) this happens in such a manner as to bound the maximum possible loss incurred by the market maker, no matter how large the order size, (iii) contracts that are obvious complements, such as "Lincoln to win Best Picture" and "Lincoln not to win Best Picture" have prices that sum to 1.
What makes this market interesting is that the algorithm ensures consistency in prices across linked contracts, quickly exploiting and eliminating any arbitrage opportunities than might arise. Some of these arbitrage conditions are not immediately transparent, as the following simplified example reveals.
Suppose that there were only two Oscar categories (Best Picture and Best Director) and consider the following seven events:
Lincoln to win Best Picture
Lincoln not to win Best Picture
Lincoln to win Best Director
Lincoln not to win Best Director
Lincoln to win 0 Oscars
Lincoln to win 1 Oscar
Lincoln to win 2 Oscars
Let pi denote the price of contract i, where i = 1,...,7, where each contract pays out one dollar if the event in question occurs. Clearly we must have
p1 + p2 = p3 + p4 = 1,
otherwise there would be an arbitrage opportunity. Similarly, we must have
p5 + p6 + p7 = 1.
Price adjustments in response to orders are such that these equalities are continuously maintained. Somewhat less obviously, we must also have
p1 + p3 = p6 + 2p7.
If this condition were violated, then one could construct a portfolio that guaranteed a positive profit no matter what the eventual outcome may be. To see this, suppose that prices were such that
p1 + p3 > p6 + 2p7.
In this case, the following portfolio would yield a risk-free profit: buy one unit each of contracts 2, 4, and 6, and two units of contract 7. This would cost
(1 - p1) + (1 - p3) + p6 + 2p7 < 2.
The payoff from this portfolio would be exactly 2, no matter how things turn out. If Lincoln wins no Oscars then contracts 2 and 4 each pay out one unit, if it wins one Oscar then contract 6 pays out a unit, in addition to either contract 2 or contract 4, and if it wins two Oscars then each of the two units of contract 7 pays out.
In reality, there are more than two categories for which Lincoln has been nominated, and the arbitrage conditions are accordingly more complex. The point is that whenever trades occur that cause these conditions to be violated, the algorithm itself begins to execute additional trades that exploit the opportunity, shifting prices in such a manner as to restore parity. In peer-to-peer markets this activity is left to the participants themselves; trader developed algorithms have been in widespread use on Intrade for instance.
One problem with peer-to-peer markets is that only a few contracts can have significant liquidity, and complex combinations of events will therefore not be transparently and consistently priced. But the design described here allows for the consistent valuation of any combination of events, at the cost of subjecting the market maker to potential loss. The pricing function is designed to place a bound on this loss, but it cannot be avoided entirely because market participants have access to information that the market maker lacks.
Could this be a template for markets on compound events in the future? It certainly seems possible, if the internally generated arbitrage profits are large enough to compensate for the information disadvantage faced by the market maker. But at the moment this is a research initiative, focused on evaluating the effectiveness of the mechanism for aggregating distributed information. This goal is best served by broad participation and better data, so if you have a few minutes to spare before the Oscar winners are announced on Sunday, why not log in and place a few (hypothetical) bets?



